Consider lunch. Perhaps a nice ham sandwich. A slice of a knife neatly halves the ham and its two bread slices. But what if you slip? Oops, the ham now rests folded under a flipped plate, with one slice of bread on the floor and the other stuck to the ceiling. Here’s some solace: geometry ensures that a single straight cut, perhaps using a room-sized machete, can still perfectly bisect all three pieces of your tumbled lunch, leaving exactly half of the ham and half of each slice of bread on either side of the cut. That’s because math’s “ham sandwich theorem” promises that for any three (potentially asymmetric) objects in any orientation, there is always some straight cut that simultaneously bisects them all. This fact has some bizarre implications as well as some sobering ones as it relates to gerrymandering in politics.
The theorem generalizes to other dimensions as well. A more mathematical phrasing says that n objects in n-dimensional space can be simultaneously bisected by an (n – 1)–dimensional cut. That ham sandwich is a bit of a mouthful, but we’ll make it more digestible. On a two-dimensional piece of paper, you can draw whatever two shapes you want, and there will always be a (one-dimensional) straight line that cuts both perfectly in half. To guarantee an equal cut for three objects, we need to graduate to three dimensions and cut them with a two-dimensional plane: think of that room-ravaging machete as slipping a thin piece of paper between the two halves of the room. In three dimensions, the machete has three degrees of freedom: you can scan it back and forth across the room, then stop and rotate it to different angles, and then also rock the machete from side to side (like how carrots are often cut obliquely, and not straight).
If you can imagine a four-dimensional ham sandwich, as mathematicians like to do, then you could also bisect a fourth ingredient with a three-dimensional cut.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
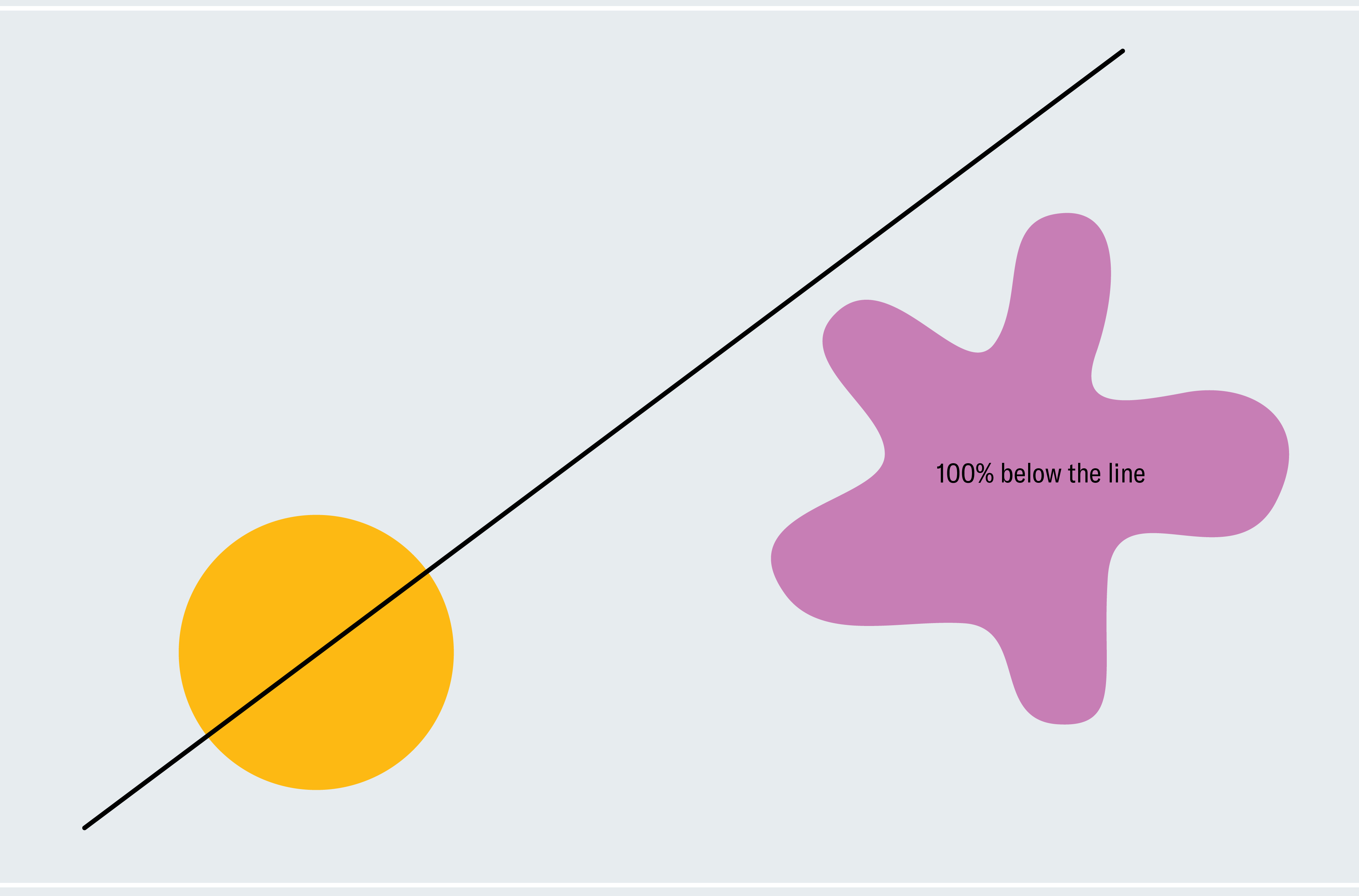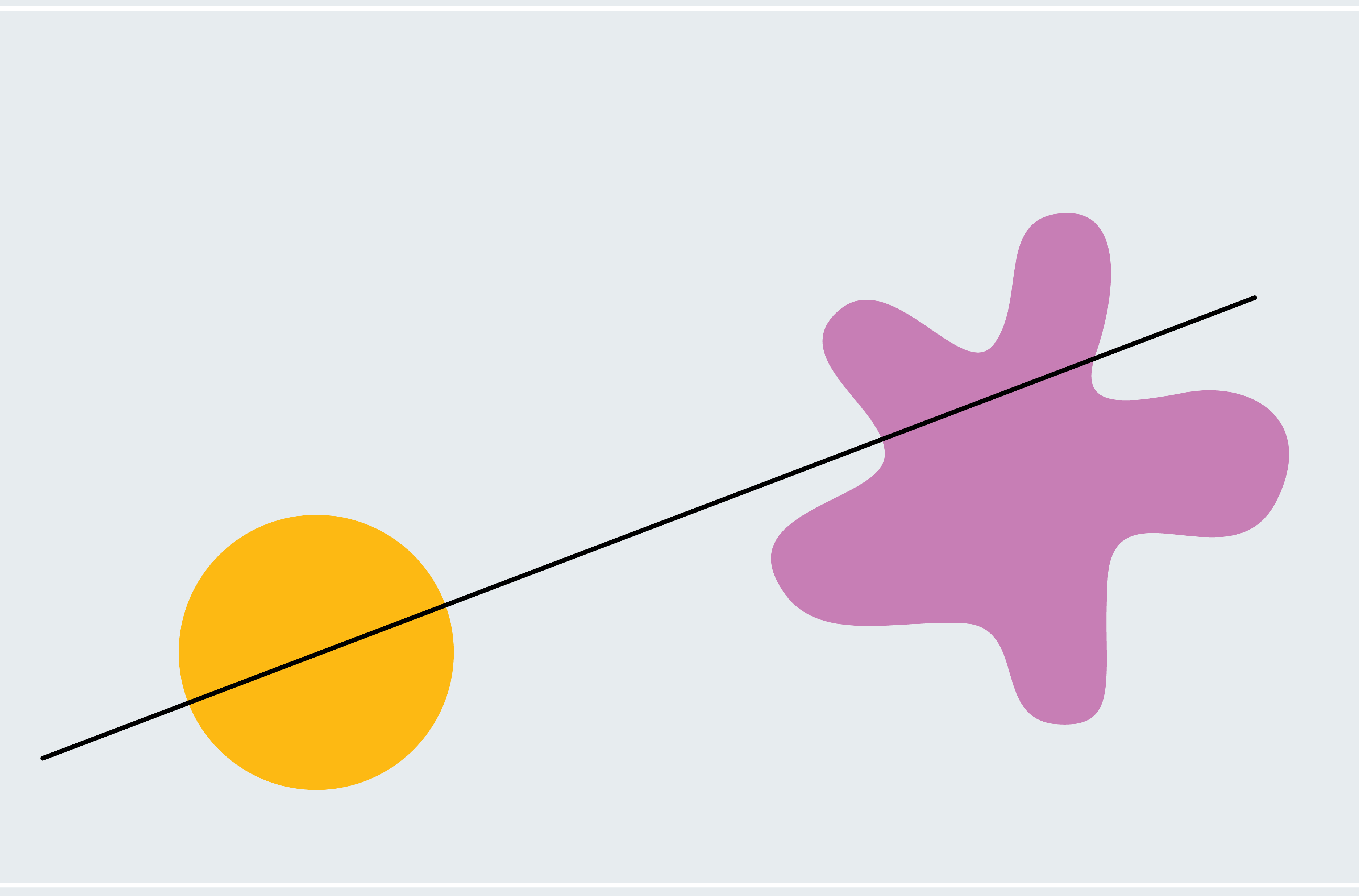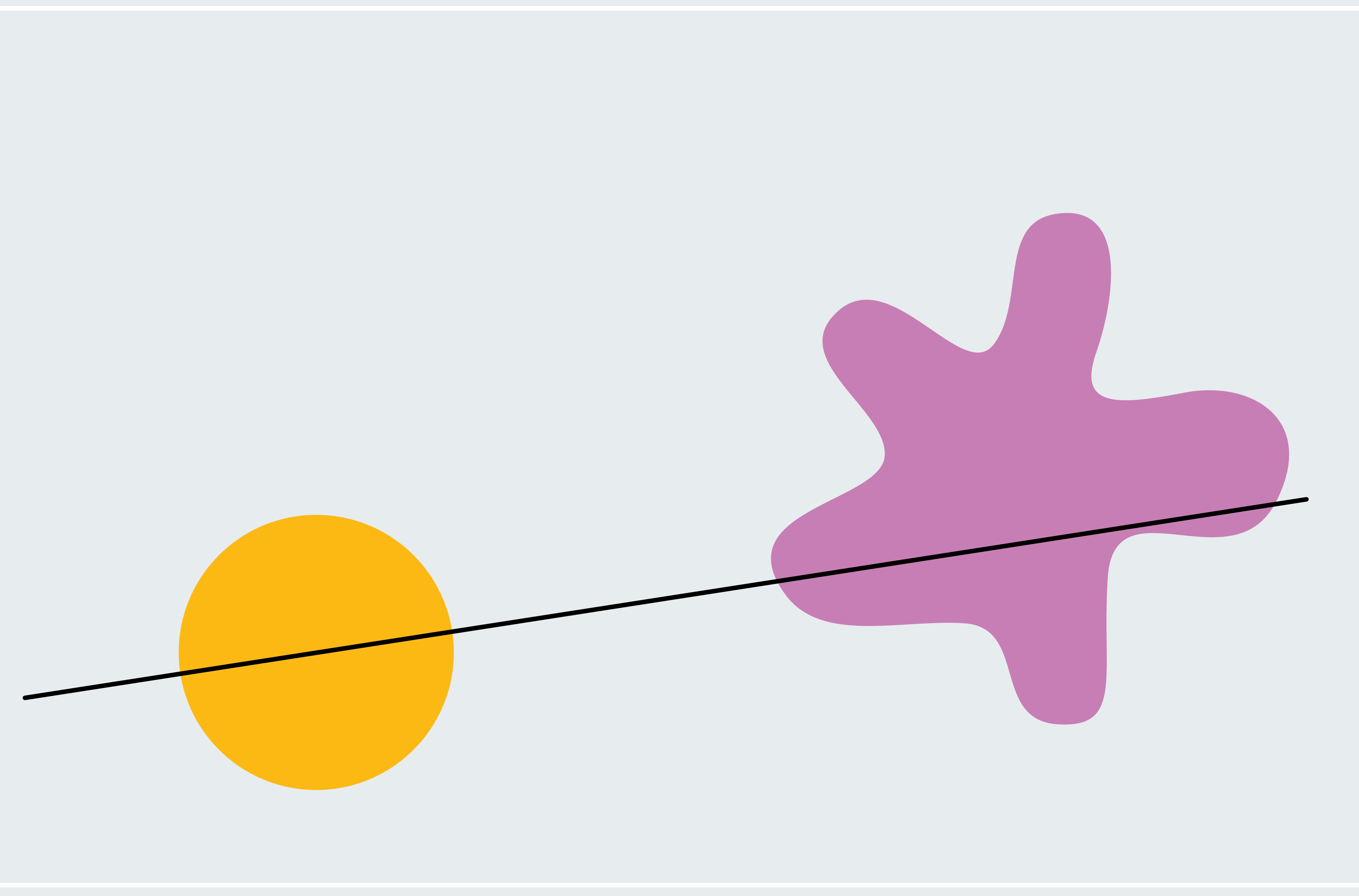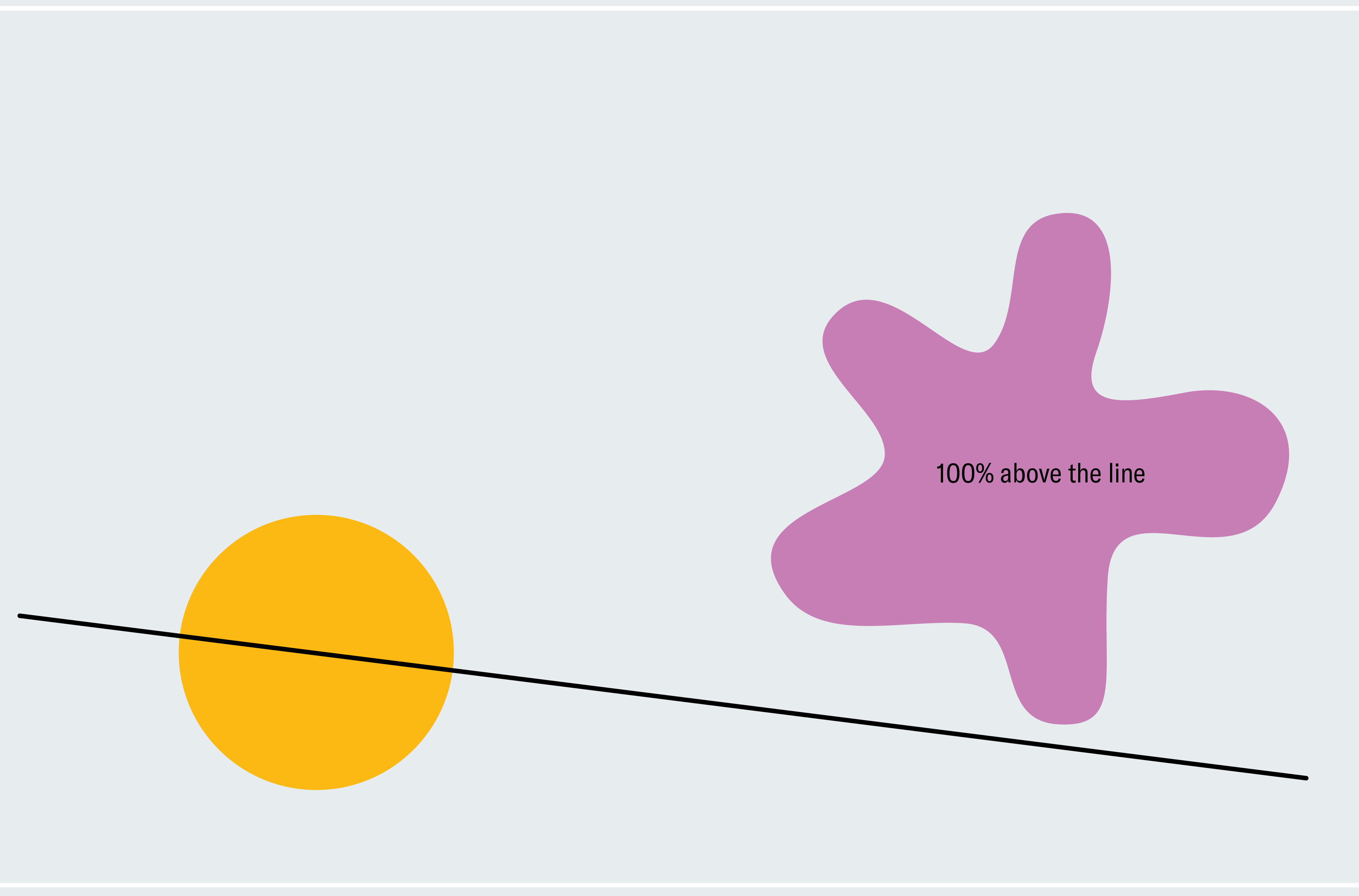
To get a flavor for how to prove the ham sandwich theorem, consider a simplified version: two shapes in two dimensions where one of them is a circle and the other is a blob. Every line that passes through the center of a circle bisects it (asymmetrical shapes don’t necessarily have a center like this; we’re using a circle to make our lives easier for now). How do we know that one of these lines also bisects the blob? Pick a line through the center of the circle that doesn’t intersect the blob at all. As depicted in the first panel below, 100 percent of the blob lies below the line. Now slowly rotate the line around the center of the circle like a windmill. Eventually, it breaches the blob, cuts through more and more of it, and then passes below it where zero percent of the blob lies below the line. From this process, we can deduce that there must be a moment at which exactly 50 percent of the blob lies below the line. We’re gradually moving from 100 percent down continuously to zero percent, so we must pass every amount in between, meaning at some point we are at exactly 50 percent (calculus fans might recognize this as the intermediate value theorem).
This argument proves that there is some line that simultaneously bisects our shapes (although it doesn’t tell us where that line is). It relies on the convenient fact that every line through the center of a circle bisects it, so we could freely rotate our line and focus on the blob without worrying about neglecting the circle. Two asymmetric shapes require a subtler version of our windmill technique, and the extension to three dimensions involves more sophisticated arguments.
Interestingly the theorem holds true even if the ham and bread are broken into multiple pieces. Use a cookie cutter to punch out ham snowmen, and bake your bread into croutons; a perfectly equal cut will always exist (each snowman or crouton won’t necessarily be halved, but the total amount of ham and bread will be). Taking this idea to its extreme, we can make a similar claim about points. Scatter your paper with red and green dots, and there will always be a straight line with exactly half of the reds and half of the greens on either side of it. This version requires a small technicality: points that lie exactly on the dividing line can be counted on either side or not counted at all (for example, if you have an odd number of reds then you could never split them evenly without this caveat).
Contemplate the bizarre implications here. You can draw a line across the U.S. so that exactly half of the nation’s skunks and half of its Twix bars lie above the line. Although skunks and Twix bars are not actually single points, they might as well be when compared to the vast canvas of American landmass. Kicking things up a dimension, you can draw a circle on Earth (slicing through a globe leaves a circular cross section) that contains half of the world’s rocks, half of its paper, and half of its scissors, or any other zany categories you wish.
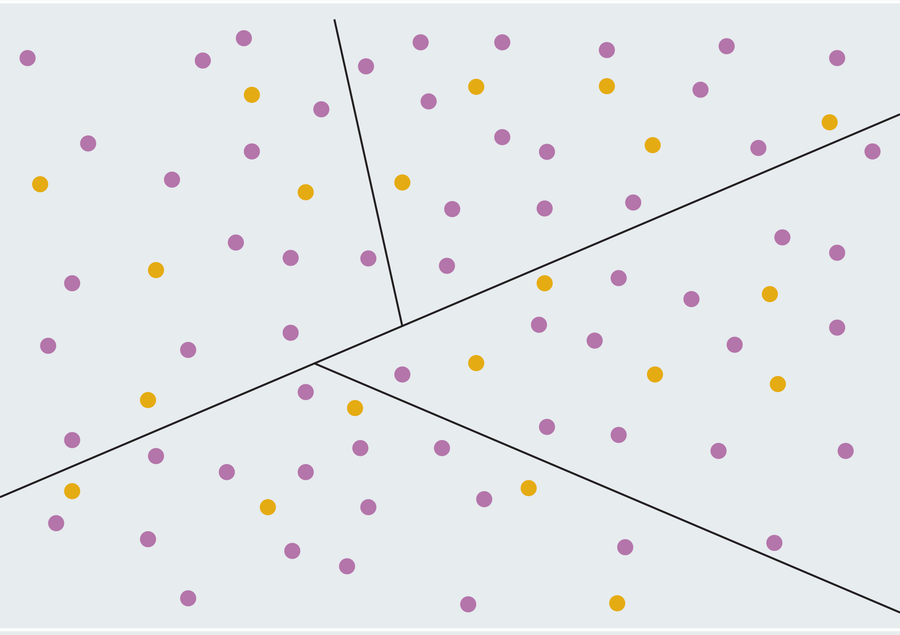
As mentioned, the ham sandwich theorem carries far less whimsical consequences for the perennial problem of gerrymandering in politics. In the U.S., state governments divide their states into electoral districts, and each district elects a member to the House of Representatives. Gerrymandering is the practice of carving out these district boundaries deliberately for political gain. For a simplified example, imagine a state with a population of 80 people. 75 percent of them (60 people) favor the purple party, and 25 percent (20 people) prefer the yellow party. The state will be divided into four districts of 20 people each. It seems fair that three of those districts (75 percent) should go to purple and the other one should go to yellow so that the state’s representation in Congress accords with the preferences of the population. However, a crafty cartographer could squiggle district boundaries in such a way that each district contains 15 purple-voters and five yellow-voters. This way, purple would hold a majority in every district and 100 percent of the state’s representation would come from the purple party rather than 75 percent. In fact, with sufficiently many voters, any percentage edge that one party has over another (say 50.01 percent purple vs. 49.99 percent yellow) can be exploited to win every district; just make it so 50.01 percent of every district supports the majority party.
Of course those districts look highly artificial. A seemingly obvious way to curtail gerrymandering would be to place restrictions on the shapes of the districts and disallow the tentacled monstrosities that we often see on American electoral maps. Indeed many states impose rules like this. While it might seem like mandating districts to have “normal” shapes would go a long way in ameliorating the problem, clever researchers have applied a certain geometric theorem to show how that’s a bunch of baloney. Let’s revisit our example: 80 voters comprising 60 purple-supporters and 20 yellow-supporters. The ham sandwich theorem tells us that no matter how they’re distributed, we can draw a straight line with exactly half of the purple voters and half of the yellow voters on either side (30 purple and 10 yellow on both sides). Now treat each side of the cut as its own ham sandwich problem, splitting each half with their own straight line so that every resulting region contains 15 purples and five yellows. Purple now has the same gerrymandered advantage as before (they win every district), but the resulting regions are all simple with straight-line boundaries!
Repeated ham sandwich subdivision will always produce relatively simple districts (in math-speak they’re convex polygons except where they potentially share a boundary with an existing state border). This means that basic regulations on the shapes of congressional districts probably can’t preclude even the worst instances of gerrymandering. Although math and politics may seem like distant fields, an idle geometric diversion taught us that the most natural-sounding solution to gerrymandering doesn’t cut the mustard.